visuallooki.blogg.se

Uh Notice over here at X equals one uh to function uh is continuous at that point. So here is the graph of our piecewise defined function. We can make it a little bit bolder by clicking on this. So we'll drop this keypad and we'll move this in two. Uh And then the other piece of this piecewise defined function F of X is equal to two eps when one is left and X or in other words X is greater than one, where we could just put in as it's given one is less than X. Uh So we bring up this little keypad, here's uh less than or equal to one, and then we will close those little curly brackets.

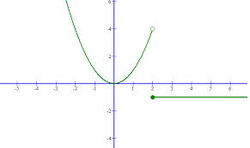
Uh So we have to use these little curly brackets and we're going to put X Less than or equal of one. Uh So f of X equals three minus x when X is less than or equal to negative one. We're going to use days most grave and calculator to help us do this. Therefore the range of the piecewise function is also the set of all real numbers greater than or equal to $0$, or all non-negative values: $y \geq 0$.To graph the piecewise defined function uh F of X is equal to three minus x. Even though there looks like a gap from $y=1$ to $y=2$, the piece of the function $f(x)=x^2$ includes those values. The range begins at the lowest $y$-value, $y=0$ and is continuous through positive infinity.

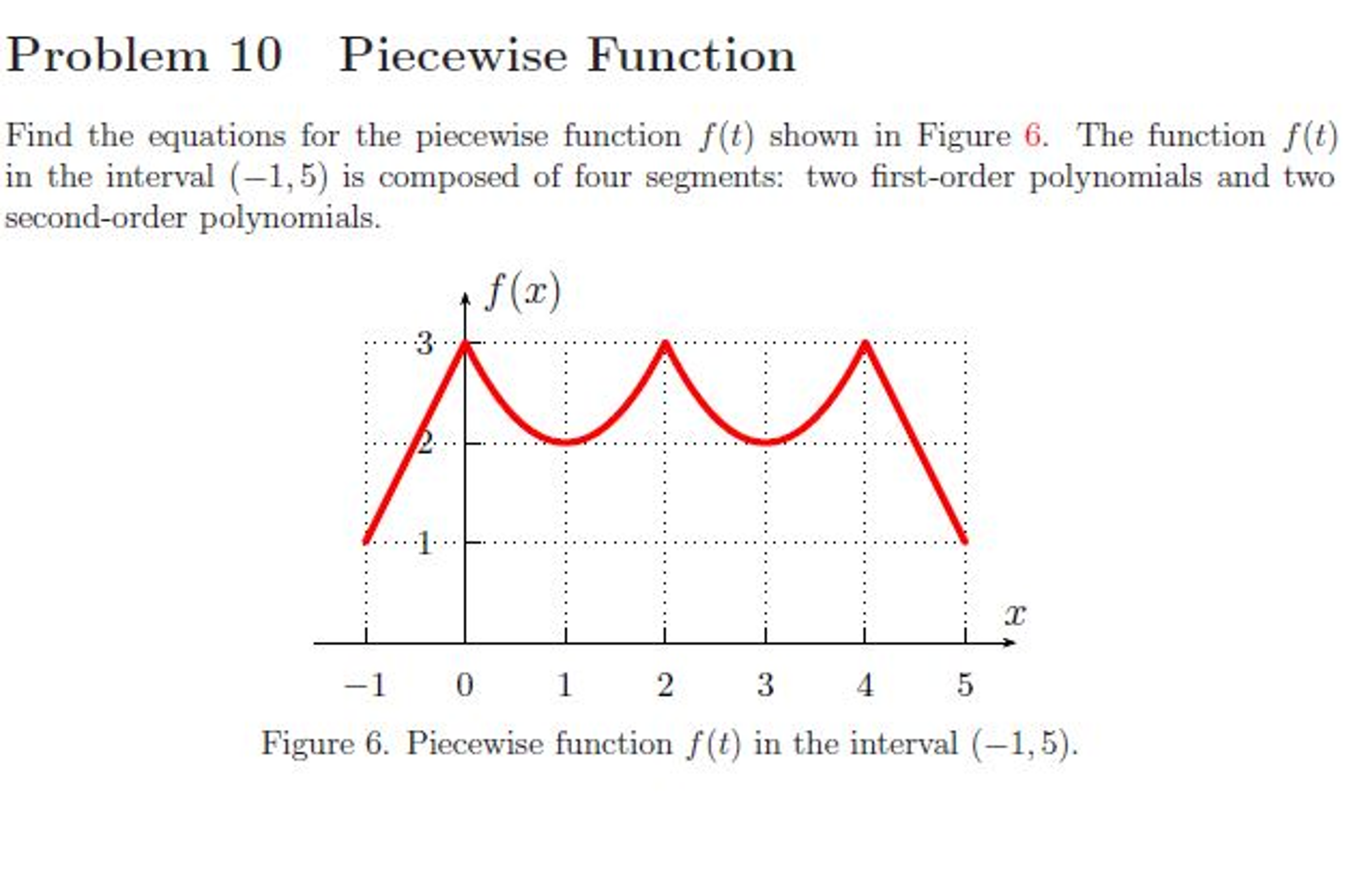
Graphing Piecewise Functions Example 1: Consider the piecewise definition of the absolute value function: We use piecewise functions to describe situations in which a rule or relationship changes as the input value crosses certain “boundaries.” Piecewise functions are defined using the common functional notation, where the body of the function is an array of functions and associated intervals. Is a function in which more than one formula is used to define the output over different pieces of the domain. Piecewise functions are defined using the common functional notation, where the body of the function is an array of functions and associated subdomains. A closed circle means the end point is included.Ī domain that is part of a larger domain.įor a real number, its numerical value without regard to its sign formally, $-1$ times the number if the number is negative, and the number unmodified if it is zero or positive.Ī function in which more than one formula is used to define the output over different pieces of the domain. strictly less than or strictly greater than. An open circle at the end of an interval means that the end point is not included in the interval, i.e.A horizontal gap means that the function is not defined for those inputs.

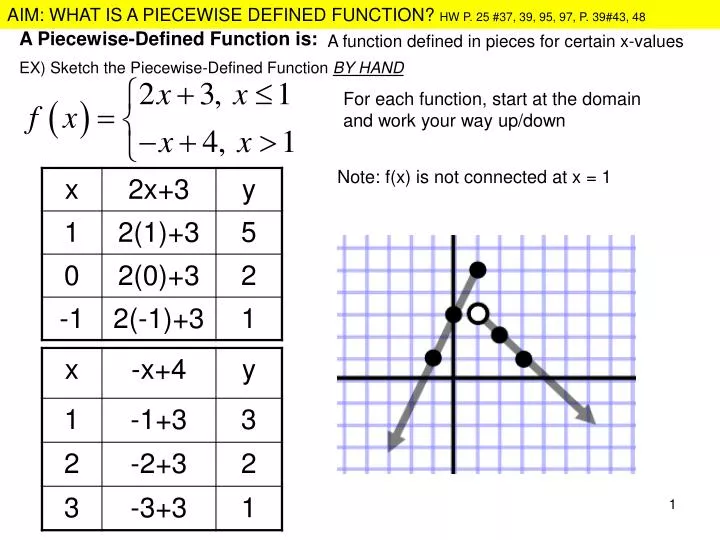
Piecewise functions may have horizontal or vertical gaps (or both) in their functions.Of course, a piecewise function can have two. It may also have extrema (maximum or minimum values), including at its endpoints. A piecewise function may have an inverse if it is one-to-one. A piecewise function may or may not be continuous or differentiable. For a real number, its value is $-x$ when $x<0$ and its value is $x$ when $x\geq0$. A piecewise function is defined by multiple functions, one for each part of a domain. The absolute value, $\left | x \right |$ is a very common piecewise function.Piecewise functions are defined using the common functional notation, where the body of the function is an array of functions and associated subdomains.